Pokemon Partner Calculator
One of the most important pieces of a good competitive Pokemon team is having Pokemon that have synergy with each other. For those who are not super familiar with Pokemon, each Pokemon has two types that are super effective and not very effective against each other. Two Pokemon have good synergy if each one covers the other Pokemon's weaknesses. For instance, a great partner for an Ice/Water type Pokemon would be Steel/Fairy, since Ice and Water are super effective against both of Steel/Fairy's weaknesses (Fire and Ground), and Steel and Fairy are super effective to 2 of Ice/Water's four weaknesses (Grass and Rock).
This is all well and good, but there are a lot of Pokemon type combinations- 324 to be exact. Plus, if we're trying to compare them with another Pokemon, that's a whopping 104,976 combinations! That's far too many to go over by hand... but that's a tiny number for a computer!
So that's what I set out to do, calculate what Pokemon have the best of what I call a "synergy" value. This value ranges from 0 to 1, with zero meaning the two Pokemon are horrible partners, and one meaning that they're perfect partners that cover each other perfectly.
PART 1: Data Storage
The first thing I had to do was figure out how to store all this data that I was going to calculate. I needed the data to be easily accessible, and I wanted to be able to export it easily for later use. This seemed like a perfect job for JSON! I made a four dimensional array within my JSON variable- with each dimension being the 18 Pokemon types. This meant that I had every combination of four Pokemon types. In retrospect, there are a lot of duplicates within this chart... Both Rock/Water and Water/Rock have a separate spot in the data, despite being mathematically identical. However, when dealing with (respectively) small numbers, this extra data isn't a huge deal. Great! I had my storage system, now I needed to do some calculations.
PART 2: Mathematics
When I started this project, I had no idea how I wanted to judge each Pokemon's synergy. It's somewhat arbitrary to take two types and compare them with just math- but I did my best to do it as sound as possible. The first thing I knew I had to do was account for the fact that different types have a different number of strengths and weaknesses- which meant I had to get a percent rather than a straight up value. One example of why this is important is Ice/Grass types. Ice/Grass is a horrible type combination, being weak to seven different types in the game.- However, since it's weak to more types, there was a higher chance that a partner would be able to cover one of those types, and thus it would show up more in my data. Clearly, having a large amount of weaknesses is not good, so we needed to look at the percentage rather than the raw number. The percentage I took was the number of weaknesses that the partner Pokemon was able to cover, divided by the total number of weaknesses (with two points being given to a x4 super effective move). This leveled the playing field and allowed me to look at the next step. I had two points, one for Pokemon A in respects to B, and vice version, and I had to combine them together... but what would be the best way to do it?
PART 3: Means
When I began this project a week ago, I was only aware of one kind of mean: the arithmetic mean. This is the classic mean, where you add all the items together and divide it by the number of items. Initially, this is what I wanted to use to combine two different scores, but I quickly realized that that wasn't what I was looking for. It simply gave too much credit for any situation where one of the values was zero. I began to 3D graph the equations, as it was the best way for me to visualize what was going on with three variables:
It's important for this function that any value of zero should result in a value of zero. After some tinkering, I found an equation that "folded" the square graph of the average so that the edges touched zero. This made it so that any Pokemon that didn't cover any of it's partner's weaknesses was thrown out. Here is the resulting graph:
This mean was good enough for me at the time, and I continued on with the project. However, later that week, I was watching an interesting video about "Squircles" (a combination of a square and a circle). One of the things they talked about was a different kind of mean known as the "Geometric" mean. This mean, instead of adding all the variables and dividing them, multiplies all the numbers together and then takes the square root. This was exactly what I was looking for! Don't you love it when you find a solution in a place you didn't expect? I graphed this new mean, and it was very close to my custom mean, but there was an exponential descent to zero on the sides, rather than a linear one.
The 3D graph of the geometric mean between two variables.
Now it was time to move on to actually displaying my data!
PART 4: How to view in four dimensions
I had my data, I had my combination function- now it was time to actually get some data! This part was simple, just parse through all the combinations, calculate the values, and put it in the JSON variable. Simple enough. But the issue is that we're dealing with four dimensions. 3D graphing this would be super tricky, much less 4D graphing... Which means we need to set two of the variables in order to make a 2D graph. Fortunately for us, we already have two preset variables as an input and we can graph the output in a 2D array! Our two input variables are the two types of the Pokemon that we want to find a partner for, and our output grid shows us all the different combinations and what their scores are. My Java program outputs a chart, which I can copy over to a Google Sheet that I specifically set up for this. From there, I can see with a heat map which Pokemon are the best partners.
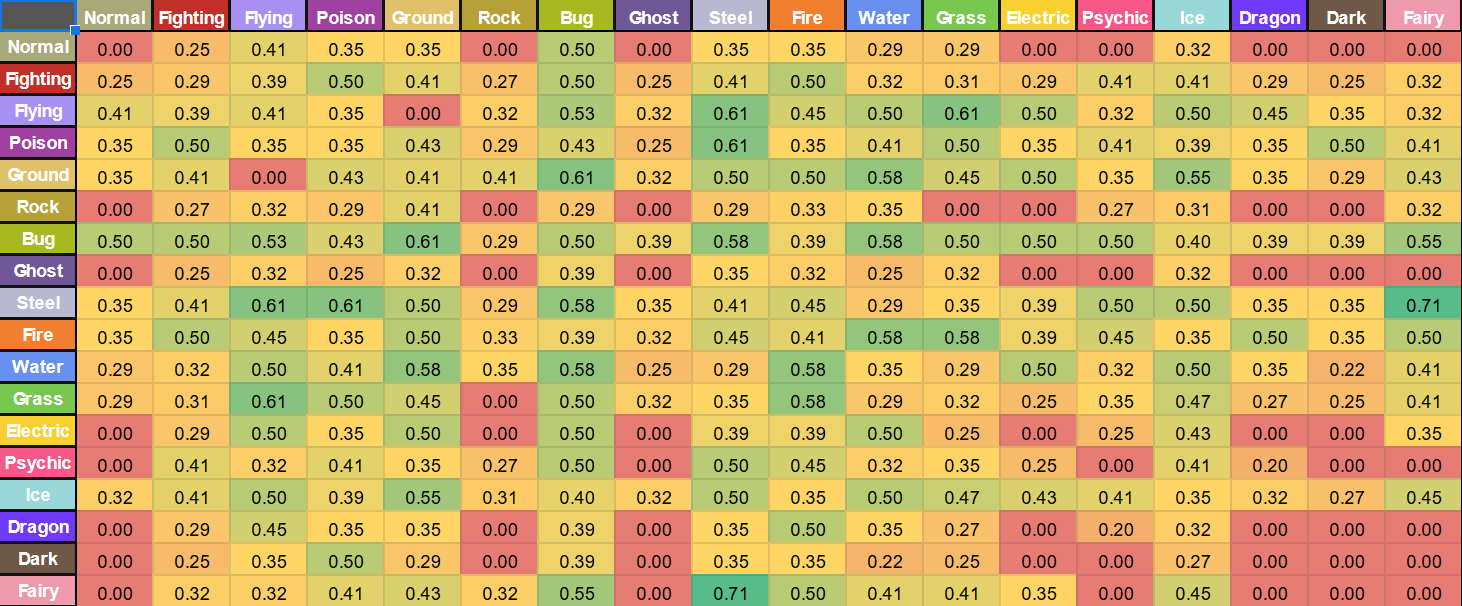
Going off my example from earlier, let's take a look at the chart for a Water/Ice type Pokemon:
Looking at this chart, we can see which type combinations have a favorable partnership with Water/Ice! In our example earlier, I mentioned Steel/Fairy, which we can see here has a rating of 71%. Not bad! Honestly, it surprises me how many good types pairings there are for Ice/Water, with a lot of them at least at 50% and above! So, now we have a team consisting of an Ice/Water Pokemon and a Steel/Fairy Pokemon... but what if I want to add a third member?
PART 5: 3 is a magic number
Fortunately for us, there's a simple way to find Pokemon that are partners with two or more other Pokemon! We just need to combine the two charts together, again using the geometric mean. So, let's do just that for our paring of Ice/Water and Steel/Fairy, and see what we get!
Wow- that's a lot of zeros! That does make a lot of sense though, because any time either chart had a zero, the output would also be zero. You'll also notice that the largest number is much lower- only 0.30. This also makes sense since there's a lot more types at play, and it's harder to find a partner that is covered by, and also covers, a pair of Pokemon. For the sake of not repeating a type, let's take a look at Grass/Flying- sitting at a decent score of 0.27. Grass/Flying covers 3 of Ice/Water's weaknesses- Rock, Grass, and Fighting, and Grass/Flying covers one of Steel/Fairy's two weaknesses- Ground. On the flip side, Grass/Flying's weaknesses of Flying, Rock, and Fire are all covered by Ice/Water, and Rock is also covered by Steel/Fairy. Clearly, it's partnership with Ice/Water is carrying the value a bit here. Nonetheless, there is synergy on all fronts, thanks to the geometric mean!
PART 6: The very best that ever was
So we're able to view what Pokemon make great partners, and we can even combine multiple charts together to see trios that work well together. But I have one more question I want answered- what is the best pair of Pokemon. What pairing has the highest score? To do this, I added a new bit to my code that checks every single value in the sheet and adds it to a list. This list will only keep the top 25 scores, since it's probably not a good idea to store over a hundred thousand values in a list and then sort through it. After running the code, here they are:
Electric/Ground & Grass/Fire [1.00]
Fairy/Steel & Dragon/Water [1.00]
Steel/Flying & Dark/Ground [0.91]
Grass/Ground & Bug/Rock [0.91]
Ground/Normal & Steel/Flying [0.87]
Electric/Grass & Fire/Ground [0.87]
Grass/Rock & Fire [0.87]
Grass/Rock & Fairy/Fire [0.87]
Electric/Water & Ice/Electric [0.87]
Grass/Fire & Rock/Ground [0.83]
Would you look at that, there's not one but two pairs that cover each other completely! And even beyond that, a score of 0.83 isn't bad either! Funnily enough, Grass/Rock and pure Fire make a great team, since Grass covers all of Fire's weaknesses, and Fire covers three of the four weaknesses that Grass/Rock has!
PART 6: Conclusion
Wow, that was a lot. Not only were we able to find some Pokemon that work perfectly as partners, we learned something along the way! But this doesn't have to be the end of the program... since technically a Pokemon can learn four moves. Currently, I'm assuming in my code that each Pokemon only knows moves that match it's two types... Maybe in the future I'll have to beef up the program and try it with each Pokemon having four different moves! That would be over eleven billion (11,019,960,576 to be exact) different combinations, so it's definitely something I'll need to compute once and then store in a file. Guess we'll just have to wait and see!
Until then, thanks for reading!
The 3D graph of my custom mean between two variables.
The 3D graph of the arithmetic mean between two variables.